| حل دستگاه معادلات به روش تجزیه LU در متلب | |
| تعداد صفحات | ۵ |
| نوع فایل | Word+PowerPoint+Matlab |
| حجم فایل | ۲۶۳ kb |
حل دستگاه معادلات به روش تجزیه LU در متلب
در این قسمت پروژه با موضوع حل دستگاه معادلات به روش تجزیه LU در متلب به صورت فایل فشرده برای دانلود ارائه شده است. کدها به همراه مثال کاربردی ارائه شده اند. توضیحات به صورت PowerPoint برای ارائه آماده شده اند.
توضیحات پروژه در زیر نشان داده شده است.
حل دستگاه معادلات به روش تجزیه LU در متلب
مشابه با روش حذفی گاوس برای حل دستگاه معادلات، روش تجزیه ال یو نیز یک روش مستقیم مشابه با این روش میباشد. در این بخش نحوه حل دستگاهها با استفاده از روش تجزیه LU را برای یک ماتریس ۳×۳ بیان نموده که قابل تعمیم برای هر دستگاه n×n خواهد بود.
اگر دستگاه معادلات دلخواهی را به فرم ماتریسی زیر تبدیل نماییم و با جابهجایی بردار b خواهیم داشت:
![]()
فرض نمایید که بتوانیم معادله بالا را بصورت یک دستگاه معادله بالامثلثی بصورت زیر برای یک ماتریس ۳*۳ بیان نماییم:
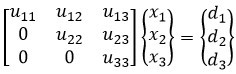
رابطه ماتریسی بالا را میتوانیم به فرم زیر بنویسیم:
![]()
فرض نمایید که ماتریس پایین مثلثی با المانهای قطری واحد را بصورت زیر داشته باشیم:
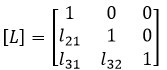
با توجه به تعریفی که از روش تجزیه LU در بخش مقدمه داشتیم، اگر این ماتریس را در معادله ماتریس بالامثلثی ضرب نماییم؛ خواهیم داشت:
![]()
در این مرحله اگر ضرب را انجام دهیم و دو طرف تساوی را برابر هم قرار دهیم:
![]()
خب با توجه به دو رابطه بالا برای حل دستگاه معادلات خطی به روش تجزیه ال یو در متلب گامهای زیر را طی میکنیم:
۱- ابتدا ماتریس بالامثلثی U با روش حذفی روبهجلو(Forward Elimination) تولید میشود.
۲- سپس ماتریس L (در بخش بعد توضیح داده میشود.) تولید میشود.
۳- با استفاده از روش جایگزینی رو به جلو (Forward Substitution) بردار d محاسبه میشود.
۴- در نهایت با استفاده از روش جایگزینی عقبی (Back Substitution) بردار x بدست میآید.
روند شماتیک این روش بصورت زیر ارائه میشود. حتما توصیه میکنیم برای فهم بیشتر این روش مطالب روش گاوس سایدل در متلب که در بالا لینک آن آمده است، را مطالعه نمایید.
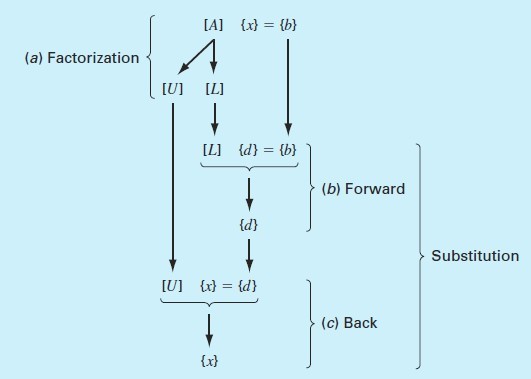
محاسبه ماتریس L برای حل دستگاه معادلات به روش تجزیه ال یو در متلب
تنها بخش ممکن برای حل دستگاه معادلات به روش تجزیه LU محاسبه ماتریس L میباشد. اگر روش حذفی گاوس را مطالعه کرده باشید، برای حذف کردن المانهای زیر قطر اصلی و ایجاد ماتریس بالامثلثی U ضریبی از سطر پایه را از سطر مربوطه تفریق میکردیم تا المان مربوطه را صفر نماییم. برای مثال ماتریس زیر را در نظر بگیرید. این ضرایب بصورت زیر محاسبه خواهند شد:
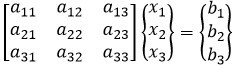
برای صفر کردن المانهای زیر المان قطری اول(a21 , a31) ضرایبی که گفته شد، بصورت زیر تعریف میشود:
![]()
بعد از صفر کردن دو المان زیر قطر در ستون اول، مقدار المانهای ماتریس تغییر میکنند. بعد از آن باید المان a32 صفر شود تا ماتریس U تشکیل شود. بنابراین ضریب مربوطه بصورت زیر تعریف میشود:
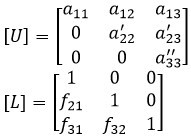
خب حال میتوانیم برای این ماتریس بردار U و L را میتوانیم بصورت زیر تعریف نماییم:
![]()
جابهجا نمودن المان قطری در حل دستگاه معادلات خطی به روش تجزیه ال یو در متلب
حل دستگاه معادلات به روش تجزیه LU در متلب ممکن است دچار مشکل شود. این روش در حل بعضی دستگاهها میتواند دچار مشکل شود به این دلیل که اگر درایههای قطری (غیر از المان قطری آخر) صفر باشند چون عبارت تقسیم بر صفر ایجاد میشود، حل دستگاه دیگر به این روش ممکن نیست. همچنین اگر المانهای قطری خیلی کوچک باشند به ازای هر تقریبی که در یکی از مجهولها ایجاد کنیم مثلا با دو رقم اعشار رند نماییم؛ مجهول دیگر به مقدار قابل توجهای تغییر میکند که باعث میشود خطای بسیار زیادی در حل دستگاه وجود داشته باشد.
برای حل این مشکل قبل از اینکه بخواهیم درایههای غیرقطری ماتریس تکمیل یافته را حذف نماییم هر ستون ماتریس را چک نموده و المانی که بیشترین مقدار را به لحاظ قدرمطلق داشته باشد، پیدا نموده و کل سطر آن را با سطر مرتبط با المانهای قطری جابهجا مینماییم. اصطلاحا به این عمل partial pivoting گفته میشود. این کار باعث میشود، هر دستگاهی با المانهای قطری صفر را نیز بتوانیم با این روش حل نماییم. همانطور که میدانید جابهجایی سطرها در حل دستگاهها، تغییری در جواب ایجاد نمیکند.
| حل دستگاه معادلات به روش تجزیه LU در متلب | |
| تعداد صفحات | ۵ |
| نوع فایل | Word+PowerPoint+Matlab |
| حجم فایل | ۲۶۳ kb |